Surjektivität, Injektivität und Bijektivität

Jetzt neu bei Alwy Allwissend: E-Learning-Inhalte – Lernen einmal ganz anders

Ob auf der Schule oder der Universität – irgendwann muss sich fast jeder einmal mit der Frage auseinandersetzen, ob eine mathematische Funktion surjektiv, injektiv oder gar beides, also bijektiv, ist. Aus unerfindlichen Gründen wird das Thema leider oftmals total kompliziert erklärt, was wohl zum Teil auch der schwer verständlichen Fachsprache geschuldet ist.

Vorbemerkung

Dieser Beitrag wird im Folgenden erklären, wie eine Funktion graphisch auf Surjektivität, Injektivität und Bijektivität untersucht werden kann. Eine mathematische Untersuchung kann in diesem Beitrag nicht erörtert werden, hierzu sei auf die zahlreiche Literatur verwiesen.

Definitionsbereich und Zielmenge

Bei jeder Aufgabe zur Beurteilung von Surjektivität, Injektivität und Bijektivität wird eine Funktionsvorschrift gegeben.

Ein Beispiel hierfür wäre:
f :
R → R
x → f (x) = x²

In der erste Zeile steht nach dem „f:“ zuerst der Definitionsbereich und anschließend die Zielmenge der nachfolgenden Funktion. Das erste R bedeutet, dass man für x jeden Wert einsetzen darf, der in den reellen Zahlen (z.B.: -1, 0, 1, 3/4, -1/2) enthalten ist und das zweite R bedeutet, dass die y-Werte, die herauskommen, wenn man ein beliebiges x aus R einsetzt, auch wieder in R liegen.

Die zweite Zeile gibt einem an, welche Funktion betracht werden soll. In diesem Fall ist dies x².

Da sich unsere Beispielfunktionsvorschrift gut eignet, die verschiedenen Fälle zu besprechen, wird sie im Folgenden
weiterverwendet.

Wann ist eine Funktion surjektiv?

Eine Funktion ist surjektiv, wenn jeder mögliche y-Wert in der Zielmenge angenommen wird.

Um zu sehen, ob dies bei unserer Beispielfunktionsvorschrift der Fall ist, wird eine Skizze von der Funktion erstellt:

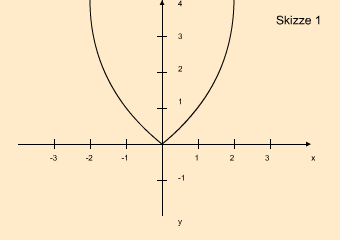
Auf der Skizze ist schön zu sehen, dass es y-Werte gibt, die nie angenommen werden können. Der y-Wert -1 z.B. wird nie angenommen werden, da die Funktion nur oberhalb der y-Achse verläuft.

Da eine Funktion aber nur surjektiv sein kann, wenn wirklich alle möglichen y-Werte angenommen werden, ist die Funktion bei der gegebenen Funktionsvorschrift nicht surjektiv.

Die gleiche Funktion würde surjektiv werden, wenn sich die Funktionsvorschrift in der ersten Zeile wie folgt ändern würde:

f : R → R₊

Eine neue Skizze zeigt es:

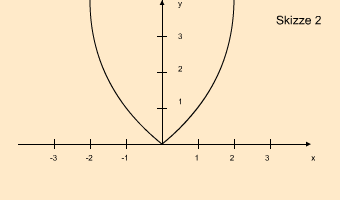
Dadurch, dass die Zielmenge nur noch aus R₊ besteht, also nur
noch aus y-Werten*, die oberhalb der y-Achse liegen, ist die gleiche Funktion nun surjektiv. Die Skizze zeigt, dass alle möglichen y-Werte angenommen werden.

* Durch das tiefergestellte Plus wird angezeigt, dass es sich um die positiv reellen Zahlen handelt (0, 1, 3, 1/3, etc.).

Wann ist eine Funktion injektiv?

Eine Funktion ist injektiv, wenn jeder y-Wert nur maximal einen dazugehörigen x-Wert
besitzt. Die Funktion x²  mit der Funktionsvorschrift f  :
R → R
kann nicht injektiv sein, da die x-Werte -1 und 1 beide auf 1 abgebildet werden und -2 und 2 auf 4.

Die grünen Kreise auf der Skizze belegen es:

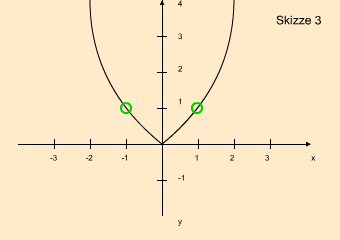
Auch wenn sich die Funktionsvorschrift zu f  : R → R₊ ändern würde, ändert sich nichts:

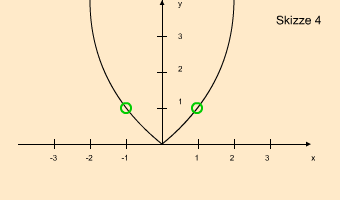
Erst wenn sich der Definitionsbereich in der Funktionsvorschrift wie folgt ändert, kann die Funktion x² injektiv werden:
f  : [0; ∞) → R₊

Das Intervall [0; ∞) bedeutet, dass für x nun nur noch Werte von 0 bis unendlich eingesetzt werden dürfen, aber keine negativen! Die Skizze zeigt, wie sich die Funktion verändert und zeigt auch deutlich, dass jeder x-Wert nun nur noch auf einem y-Wert abgebildet wird:

Und wann ist eine Funktion bijektiv?

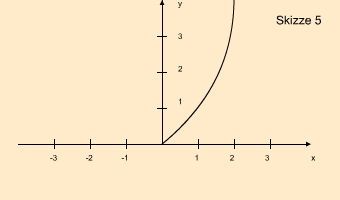
Eine Funktion ist bijektiv, wenn sie surjektiv und injektiv ist. Die Funktion x² zusammen mit dem Definitionsbereich und der Zielmenge  f  : [0; ∞) → R₊ ist bijektiv, weil sie surjektiv und injektiv ist.

Abschlussbemerkung

An dieser Stelle sollten nun zwei Aspekte des Themas deutlich geworden sein:

1. Ob eine Funktion surjektiv und/oder injektiv ist, hängt maßgeblich davon ab, wie der Definitionsbereich und die Zielmenge definiert sind.

2. Es kann je nach Definitionsbereich und Zielmenge auch Funktionen geben, die weder injektiv, noch surjektiv sind.

#E-Learning #Lernen

24. Mai 2018